

Sublime Text and Notepad++ are two great editors for coding. Sublime Text 3 is a commercial tool built by Sublime HQ, and Notepad++ is written in C++ by Don Ho. These editors run on Windows, Mac and Linux. So which is the better choice for development? And coming in at $99 USD, is Sublime Text worth paying for?
In this post I take Sublime Text up against Notepad++ using the following 7 IDE criteria:
My approach to conduct this evaluation was to pick the IDE features that I use most often and compare the experience between Notepad++ and Sublime Text 3. I use simple project examples in C and Python, HTML, CSS and Javascript to get some comparison breadth.
For this comparison I am using Sublime Text 3 installed on Ubuntu 20.04 and Notepad++ v8.1.9 on the same machine with language specific plugins when available. Notepad++ is freely available, however Sublime Text is a paid product at $99USD, which gives you 3 years of updates. Once you have a license, Sublime Text can be installed and used on as many of your systems as you like. As of the writing of this article Sublime Text has release version 4 and moving forward with semantic versioning - so no more major version releases.
My criteria for Git integration is to see how much can be done within the editor itself without the need to resort to command line. At a minimum, I expect that common actions like creating branches, committing code and managing code on remotes can be done within the IDE. I will look at both Git and GitHub integrations - see my article explaining the difference between git and github.
Notepad++ does not have built in Git or GitHub Integration. If you Google Notepad++ and Git, you'll find a lot of information on how to use Notepad++ as your default editor for Git. There is a plugin that integrates with Tortoise Git called GitSCM. It looks a bit complicated to get running on Notepad++ running on Ubuntu since it is running under the Wine environment and is expecting to find Windows settings, so my review is strictly applicable to Notepad++ on Windows.
On Windows I had to add the Git command to my path so it could be used via the command prompt. You may also need to set the Git.exe path in the GitSCM plugin settings. If the Git.exe hasn't been configured you will get a "file not found" error.
Below is a screenshot of my Windows settings.
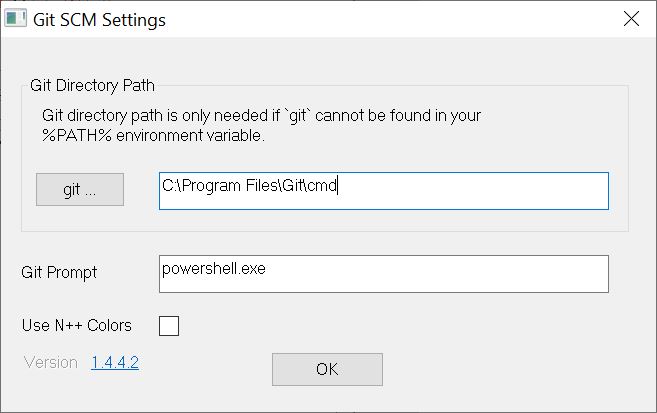
I created a new project and initialized it with Git and then added a text file to test. The docking panel provides a view of the current status of your files. Note that some actions require Tortoise Git.
So Notepad++ gets a 1/5 on Git Integration.
Git Integration in Sublime Text works best with the Git plugin. On a fresh install of Sublime you first need to install Package Control. I imagine not including package control by default helps ensure your sublime install stays as lean as possible. Install package control from the menu: Tools->Install Package Control. Once installed you can access it via Preferences->Package Control.
To install the Git plugin:
Sublime Text got stuck on the fact that my email and user name had not been configured, and was unable to handle this elegantly. Sublime Text threw up error messages and I could not commit changes. I resolved this via the git cli and was then able to commit within Sublime Text Git.
The Sublime Text Git plugin offers a lot of functionality that I usually have to Google search to remind myself of the syntax. All of the basics are there including Git Add, Git Commit - but there is also Git Reset and Git Stash. The plugin will also prompt for the various options on these commands.
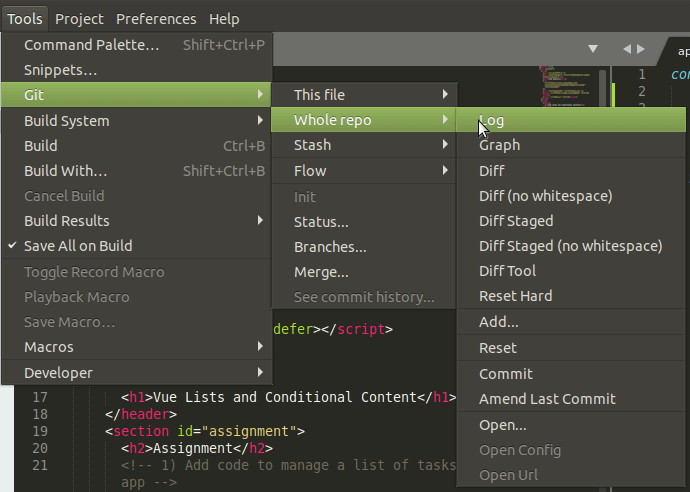
Sublime Text's Git integration is strong, it gets a 4/5.
Code management is basic functionality for an IDE, and it is important to make it easy for a developer to navigate a code base. Both Notepad++ and Sublime Text have built in file hierarchy displays on the left of the code window (with the default setup) and allow you to create, rename and remove files easily. You can select function names and quickly navigate to their definitions with both of these tools. The real differentiation is in the IDE search functionality and smart code features.
For code management there were 3 areas I focused on:
In order to test the effectiveness of Sublime Text and Notepad++ for managing projects with multifile modular designs I created a couple of simple projects in both Python and C. I also installed any popular plugins that provide appropriate language support.
For the Python project I added a file with a function definition, then called that function from my main file. I created a greet.py module with a function called greet:
def greet(name):
"""
This function greets
the person name passed in as
a parameter
"""
print("Hello, " + name + ". Good morning!")For C, a similar setup with a file containing the main function and another file with a greet function.
#include <stdio.h>
#include "greet.h"
void greet(char* name) {
printf("Hello %s, Good Morning!\n", name);
return;
}
Adding imports or header files is a bit of a distraction while coding, so the more an IDE can help remove this distraction the better.
In my Python project, when I added the 'greet' function call to my main function Notepad++ was unaware of the new function and I had to manually add the import statement. The same result for the C program, Notepad++ doesn't add the header file automatically. However, once you add the import statement Notepad++ provides auto complete on the functions it finds within the imported file.
I often have to find code across a set of project files, and for this I really like Find in Files. Especially with a code base that I have inherited, being able to find files anywhere in a project containing a keyword within a project is essential. Notepad++ supports this type of search but it's not completely intuitive.
Notepad++ Find in Files open the following dialog box. Notice the 'Directory' field. Notepad++ does not use your current folder workspace to run the search, you have to choose the directory you want to search.
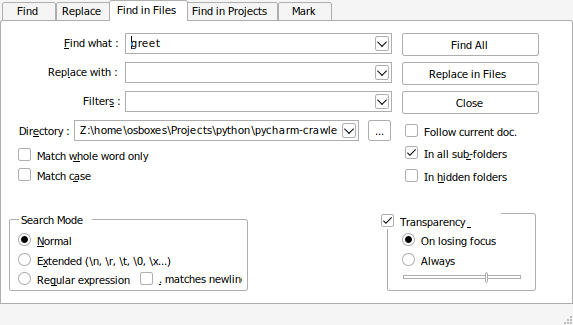
The search results are displayed in a bottom pane. Click on the search result line to open the file where the search term was found, Notepad++ will open it in the editor.
A well featured search (albeit confusing), and passable code dependency management gets Notepad++ a 3/5 on code management.
For Python development I have installed the Anaconda plugin. Note, this plugin is not associated with Python Anaconda Data Science platform.
I added another function in my greet module and called it from the hello-world file, but Anaconda did not automatically add the import statement. I guess this is a high bar for an editor - for this type of functionality you'll have to go with Pycharm.
The Find in Files search in Sublime Text also works very well. Sublime will accumulate the results of searches in the results page. To clear the results, just close the results tab.
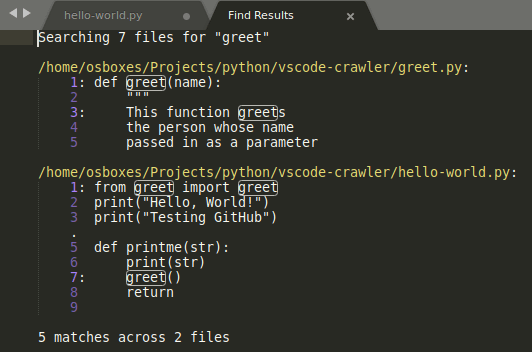
Sublime meets Notepad++ equally when it comes to code management. Because of its straightfoward search I give Sublime Text 4/5 on this category.
Syntax Highlighting is a must have feature for development, and fast and non-intrusive code completion is very helpful. Notepad++ and Sublime Text both support highlighting and code completion with plugins and extensions. Here is a summary of how Sublime Text vs Notepad++ compete.
Notepad++ supports code completion and it is quite capable.
Although Notepad++ didn't add the import statement for my new module automatically, once the import statement was added, Notepad++ offers autocomplete for this function.
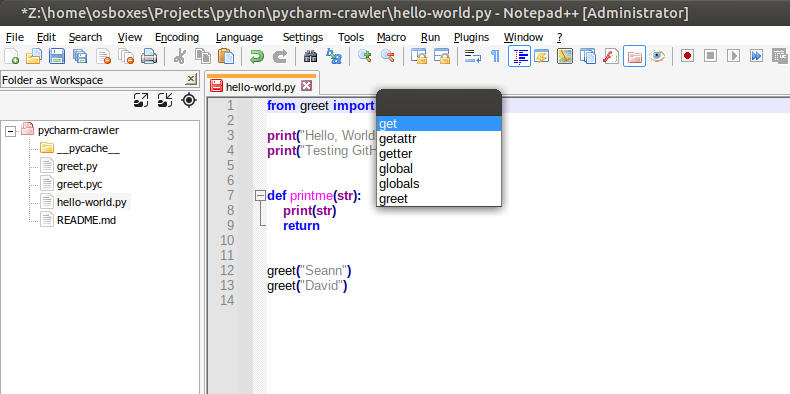
Once my code library is imported, I can type 'g' and select the greet function from a list of valid selections starting with 'g'. No other information about this function is available, like the function comment or signature, so the autocomplete is a bit limited. The code completion experience is responsive and intuitive. I would say this is a minimal code completion experience and so I rate it at 2/5.
There are language specific packages that can be installed to enable autocomplete. For Python, I have Anaconda installed.
Anaconda provides simple name lookups and displays the expected function parameters and the comment.
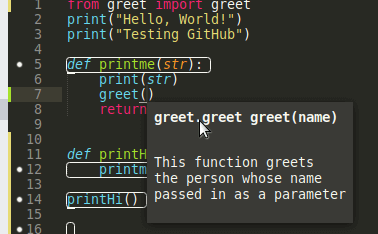
For C/C++ development, if your file has the C or CC extension Sublime will code highlight and autocomplete out of the box. One thing I noticed with Sublime Text is the autocomplete on the #include statement. Both Notepad++ and Sublime Text provide this by default.
Sublime Text's code completion gets a 3/5.
Notepad++ does not allow you to execute your code in debug mode. Debugging sits squarely in the realm of integrated development environments (IDEs) and Notepad++ is strictly a file editor.
Notepad++ does not provide a debugger and maybe rating it on this criteria isn't quite fair, however, it gets a 0/5.
Building and Debugging in Sublime requires setting up build systems. It ships with a number of build systems for common languages out of the box, and provides the ability to add new build system definitions.
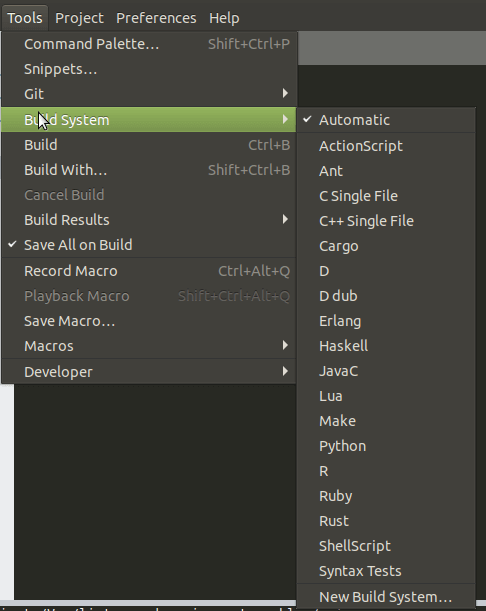
Build Systems are very handy - they allow you to build and run your code directly from Sublime Text.
For debugging in Sublime Text I have the Python Debugger package installed.
Python breakpoints can be added by selecting a line and choosing toggle breakpoint.
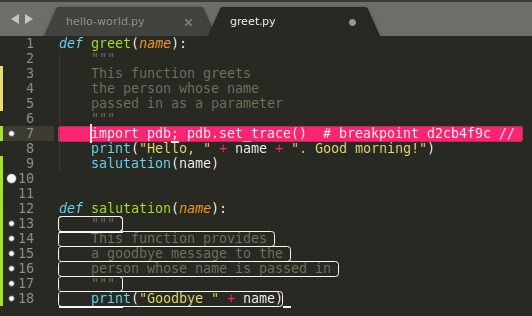
Debugging is doable and at least offers more than Notepad++, so based on my experience, I give it a 2/5.
For this test, I am running Sublime Text and Notepad++ inside of an Ubuntu VM hosted in VirtualBox. I have 4 CPU cores allocated and 4 GB of memory for the virtual machine.
Start Up time is good for Notepad++, once the VM is primed Notepad++ loads in about 3 to 4 seconds. My test project is only a couple of files, so I don't have a good sense of how it handles large projects. But it will load in the most recent file workspace which is handy. Notepad++ runs under Wine and consumes a minimal amount of memory, about 50 MB.
The Wine infrastructure occupies another 50MB between the Wine devices and the Wine Server.
Notepad++ gets a 5/5 on performance.
Sublime Text is built with C++ and Python and it shows. It loads very quickly and consumes minimal memory.
Once loaded, both IDEs were quite responsive with minimal stuttering when looking up autocomplete suggestions for example.
| Measure | Notepad++ | Sublime Text |
|---|---|---|
| Start Up Time | 4 sec (avg) | 2 sec |
| Memory Use | 100MB | 80MB |
| My Rating | 5/5 | 5/5 |
Sublime Text runs very well, even on my older systems, and leaves memory space for other applications.
Sublime Text gets a 5/5 for performance.
I may be unfairly applying this criteria to Notepad++ as refactoring support is more of an IDE feature. It is possible to use search and replace in clever ways to refactoring code, but this is more of a workaround.
Since Notepad++ refactoring capabilities are non-existant a 0/5 goes to Notepad++ for refactoring.
The Anaconda plugin has a rename object function but - I was unsuccessful in getting it work? I was also a bit disappointed when I selected goto definition on my imported function and it took me to the import statement where I had to goto definition again to get to the function declaration. Sublime didn't wow me with its refactoring power.
Sublime Text gets a 0/5 in the refactoring category.
Notepad++ is quite portable thanks to Linux Wine. It does not run on my Raspberry Pi 4 unfortunately, and since it is closed source I can't compile it for ARM.
Notepad++ runs on AMD but not ARM architectures in 32 or 64 bits. Running on Wine doesn't make it Linux Native. It is somewhat cross platform, a 3/5 here.
Notepad++ is a windows executable and is not open source so to run it on Linux, you need to host it in Wine.
Note that Notepad++ will install into the accessories group in Ubuntu and not the Programming group.
sudo snap install notepad-plus-plusSublime Text runs on Windows, Mac and Linux, but not on Raspberry Pi, or ARM for that matter. I have seen rumors regarding possible ARM support may be coming? Unfortunately Sublime Text is closed source, so it cannot be compiled to ARM by the community.
Sublime Text gets a 3/5 on cross platform because of a lack of ARM support.
Here are all the ratings for the eight categories.
| Criteria | Notepad++ | Sublime Text |
|---|---|---|
| Git Integration | 1/5 | 4/5 |
| Code Management | 3/5 | 4/5 |
| Code Completion | 2/5 | 3/5 |
| Debugging | 0/5 | 2/5 |
| Performance | 5/5 | 5/5 |
| Refactoring | 0/5 | 0/5 |
| Cross Platform | 3/5 | 3/5 |
| Total | 14/35 | 21/35 |
Because Sublime Code and Notepad++ are built with C++ they are highly performant editors.
Sublime Text is great at text file manipulation, and because it loads as quickly as Notepad++. Both editors are useful in cases where you need to update config files (XML, YAML and JSON format).
These editors are fine for some quick coding, but you would be served better by using an IDE like VSCode.
For all you Python developers, read my comparison of PyCharm and VSCode in my Pycharm vs VSCode review.
Also, check out my other editor comparisons of Atom vs VSCode and Sublime Text vs VSCode.
Photo by Jan Kahánek on Unsplash